Неуловимый эллипс: рисование эллипсов в перспективе — художественный блог

Содержание:

Определение
- Другие определения
Построение цилиндра в перспективе, вид сбоку.
- - Теперь попробуем рисовать цилиндр в перспективе.
Команда AutoCAD Эллипс (Ellipse)
Соотношения между элементами эллипса
Как начертить эллипсы по большой оси и углу поворота окружности
Процедура DrawEllipse
Если известна большая ось
Элементы черчения для начинающих — построение эллипса техническими способами.
Другие свойства
Как рисовать правильные овалы
Площадь эллипса и его сегмента

Определение

Эллипс — геометрическое место точек M евклидовой плоскости, для которых сумма расстояний до двух данных точек F1{\displaystyle F_{1}} и F2{\displaystyle F_{2}} (называемых фокусами) постоянна и больше расстояния между фокусами, то есть

|F1M|+|F2M|=2⋅a{\displaystyle |F_{1}M|+|F_{2}M|=2\cdot a}, причём |F1F2|<2⋅a{\displaystyle |F_{1}F_{2}|<2\cdot a}.

Другие определения

Эллипс также можно определить как:

фигуру, которую можно получить из окружности, применяя аффинное преобразование
ортогональную проекцию окружности на плоскость
пересечение плоскости и кругового цилиндра.

Построение цилиндра в перспективе, вид сбоку.

Особенности и советы по эксплуатации стусла для плинтусов

Положим один кирпич поверх другого. Предположим, что их торцы образуют
квадрат. Нарисуем на торцах диагонали и тем самым найдем центр. Это центр
круга, который касается всех четырех сторон квадрата.

Рис. 13.11. Построение цилиндра в черчении без
перспективы.

Этот круг можно расценивать как торец цилиндра, который проходит через всю
толщу кирпича. На противоположном торце нарисуем еще один круг.

Линия, проведенная между центрами двух окружностей, — это центральная/осевая
линия цилиндра или в нашем случае — ось двух колес. Эта ось — продолжение
коротких осей двух эллипсов и ножка двух букв Т.

Длинная ось образует перекладину буквы Т.

Мы начали с предположения, что торцы двух кирпичей, положенных один на
другой, образуют квадрат.

Теперь попробуем рисовать цилиндр в
перспективе.

Нарисуем кирпичи с применением законов перспективы. Круг, вписанный в
квадрат, становится эллипсом, касающимся сторон квадрата (нарисованного в
перспективе) в центре каждой из сторон.

Рис. 13.12. Построение цилиндра в перспективе.

Линия, проведенная через центр круга до точки схода, должна быть центральной
линией цилиндра или осью для двух колес.

Линия, проведенная через этот же центр и пересекающая эту ось под прямым
углом, будет самой длинной линией или большой осью эллипса.

Большая ось всегда образует прямой угол с центральной осью цилиндра.

Нет никакой разницы, в каком направлении лежит цилиндр и лежит ли он на боку
или стоит на торце, большая ось эллипса всегда будет образовывать букву Т с
центральной/осевой линией цилиндра. Малая ось эллипса лежит вдоль этой
центральной/осевой линии цилиндра. Малая ось эллипса становится центральной
линией цилиндра, т.е. они должны совпадать.

Рис. 13.13. Правильное положение осей эллипса цилиндра в пространстве.

Нарисуйте/начертите цилиндр с соблюдением правил перспективы. Затем
поверните бумагу так, чтобы цилиндр оказался в вертикальном положении.

Рис. 13.14. Цилиндр в перспективе в вертикальном положении.

Первое изображение цилиндра является правильным, второе — неправильное.

Команда AutoCAD Эллипс (Ellipse)

Схемы управления освещением с использованием различных типов выключателей

За создание эллипса в Автокад отвечает команда Эллипс/Ellipse, вызвать которую можно следующими способами (начать его построение):

построить эллипсы в Автокаде можно из строки меню пункт Рисование — строка Ellipse;
создать его можно из вкладки Главная ленты инструментов — в группе инструментов Рисование кнопка «Центр, (Ось, конец)», т.е. вам сразу в ленте доступны опции команды Эллипс в Автокаде;
нарисовать объект Эллипс можно из классической панели инструментов Рисование кнопка Ellipse;
а так же непосредственное создание эллипса в программе из командной строки, прописав наименование команды в командной строке Эллипс/Ellipse.

Соотношения между элементами эллипса

Монтаж гипсокартона

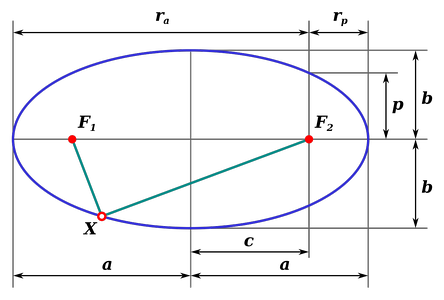Части эллипса (описание см. в разделе «Связанные определения»)

a{\displaystyle {\boldsymbol {a}}} — большая полуось;
b{\displaystyle {\boldsymbol {b}}} — малая полуось;
c{\displaystyle {\boldsymbol {c}}} — фокальное расстояние (полурасстояние между фокусами);
p{\displaystyle {\boldsymbol {p}}} — фокальный параметр;
rp{\displaystyle {\boldsymbol {r}}_{p}} — перифокусное расстояние (минимальное расстояние от фокуса до точки на эллипсе);
ra{\displaystyle {\boldsymbol {r}}_{a}} — апофокусное расстояние (максимальное расстояние от фокуса до точки на эллипсе);

a2=b2+c2{\displaystyle a^{2}=b^{2}+c^{2}};

e=ca=1−b2a2(⩽e<1){\displaystyle e={\frac {c}{a}}={\sqrt {1-{\frac {b^{2}}{a^{2}}}}}\;\;\;(0\leqslant e<1)};

p=b2a{\displaystyle p={\frac {b^{2}}{a}}}.

	a{\displaystyle {\boldsymbol {a}}}	b{\displaystyle {\boldsymbol {b}}}	c{\displaystyle {\boldsymbol {c}}}	p{\displaystyle {\boldsymbol {p}}}	rp{\displaystyle {\boldsymbol {r_{p}}}}	ra{\displaystyle {\boldsymbol {r_{a}}}}
a{\displaystyle {\boldsymbol {a}}} — большая полуось	a{\displaystyle {\boldsymbol {a}}}	a=b1−e2{\displaystyle a={\frac {b}{\sqrt {1-e^{2}}}}}	a=ce{\displaystyle a={\frac {c}{e}}}	a=p1−e2{\displaystyle a={\frac {p}{1-e^{2}}}}	a=rp1−e{\displaystyle a={\frac {r_{p}}{1-e}}}	a=ra1+e{\displaystyle a={\frac {r_{a}}{1+e}}}
b{\displaystyle {\boldsymbol {b}}} — малая полуось	b=a1−e2{\displaystyle b=a{\sqrt {1-e^{2}}}}	b{\displaystyle {\boldsymbol {b}}}	b=c 1−e2e{\displaystyle b={\frac {c~{\sqrt {1-e^{2}}}}{e}}}	b=p1−e2{\displaystyle b={\frac {p}{\sqrt {1-e^{2}}}}}	b=rp1+e1−e{\displaystyle b=r_{p}{\sqrt {\frac {1+e}{1-e}}}}	b=ra1−e1+e{\displaystyle b=r_{a}{\sqrt {\frac {1-e}{1+e}}}}
c{\displaystyle {\boldsymbol {c}}} — фокальное расстояние	c=ae{\displaystyle c=ae}	c=be1−e2{\displaystyle c={\frac {be}{\sqrt {1-e^{2}}}}}	c{\displaystyle {\boldsymbol {c}}}	c=pe1−e2{\displaystyle c={\frac {pe}{1-e^{2}}}}	c=rpe1−e{\displaystyle c={\frac {r_{p}e}{1-e}}}	c=rae1+e{\displaystyle c={\frac {r_{a}e}{1+e}}}
p{\displaystyle {\boldsymbol {p}}} — фокальный параметр	p=a(1−e2){\displaystyle p=a(1-e^{2})}	p=b 1−e2{\displaystyle p=b~{\sqrt {1-e^{2}}}}	p=c 1−e2e{\displaystyle p=c~{\frac {1-e^{2}}{e}}}	p{\displaystyle {\boldsymbol {p}}}	p=rp(1+e){\displaystyle p=r_{p}(1+e)}	p=ra(1−e){\displaystyle p=r_{a}(1-e)}
rp{\displaystyle {\boldsymbol {r}}_{p}} — перифокусное расстояние	rp=a(1−e){\displaystyle r_{p}=a(1-e)}	rp=b 1−e1+e{\displaystyle r_{p}=b~{\sqrt {\frac {1-e}{1+e}}}}	rp=c 1−ee{\displaystyle r_{p}=c~{\frac {1-e}{e}}}	rp=p1+e{\displaystyle r_{p}={\frac {p}{1+e}}}	rp{\displaystyle {\boldsymbol {r}}_{p}}	rp=ra1−e1+e{\displaystyle r_{p}=r_{a}{\frac {1-e}{1+e}}}
ra{\displaystyle {\boldsymbol {r}}_{a}} — апофокусное расстояние	ra=a(1+e){\displaystyle r_{a}=a(1+e)}	ra=b 1+e1−e{\displaystyle r_{a}=b~{\sqrt {\frac {1+e}{1-e}}}}	ra=c 1+ee{\displaystyle r_{a}=c~{\frac {1+e}{e}}}	ra=p1−e{\displaystyle r_{a}={\frac {p}{1-e}}}	ra=rp 1+e1−e{\displaystyle r_{a}=r_{p}~{\frac {1+e}{1-e}}}	ra{\displaystyle {\boldsymbol {r}}_{a}}

Как начертить эллипсы по большой оси и углу поворота окружности

После того как вы укажете большую ось эллипса в AutoCAD, в командной строке появится запрос:

Длина другой оси или :

Длина другой оси — это малая ось эллипса Автокад, если вы выберите опцию «Поворот».

Опция «Поворот» команды Ellipse позволяет повернуть окружность на определенный угол (заданная большая ось эллипса — это ось вращения окружности), проекция которой на рабочую плоскость XY является эллипсом.

Выберем опцию «Поворот». Система отобразит запрос:

Поворот относительно главной оси:

Главная ось — это заданная большая ось эллипса. Поворот относительно главной оси: — т.е. необходимо задать угол поворота окружности.

Введем в командную строку угол 180 градусов или можете ввести 0 градусов. Как только вы зададите угол поворота, эллипс в Автокад будет построен, а команда Ellipse завершит свое выполнение.

Построенный эллипс в AutoCAD представляет собой окружность, т.к. если вы ввели 0 градусов, то окружность вокруг большой оси эллипса мы не повернули и ее проекцией на рабочую плоскость XY является окружность.

Примечание
Команда Ellipse используется для вычерчивания окружностей в изометрии.

Процедура DrawEllipse

✎ — Рисует границу эллипса, ограниченного прямоугольником, заданным координатами противоположных вершин (x1, y1) и (x2, y2)

В определении сказано, что рисует только границу эллипса. Что это означает? Это значит, что такой эллипс будет как бы «полым» внутри, поэтому задавать цвет кисти Brush здесь бессмысленно. Если что-то предварительно нарисовать, а потом сверху эллипс DrawEllipse, то пространство элипса не закроет собой фигуру – нарисуется только линия.

Вот примерный код на PascalABC.Net:

Код PascalABC.Net

uses
  GraphABC;
  
var
  x1, y1, x2, y2 integer;

begin
  SetPenWidth(3); //толщина линии границы
  SetPenColor(ClRed); //цвет линии границы
  x1 := 100; y1 := 80; //координаты левой верхней вершины
  x2 := 500; y2 := 300; //координаты правой нижней вершины
  DrawEllipse(x1, y1, x2, y2) { <-- рисуем ГРАНИЦУ эллипса,
  ограниченного прямоугольником с координатами 
  противоположных вершин (x1, y1) и (x2, y2) }
end.

Заметим, что предыдущий код можно сократить до такого:

Код PascalABC.Net

uses
  GraphABC;

begin
  SetPenWidth(3); //толщина линии границы
  SetPenColor(ClRed); //цвет линии границы
  DrawEllipse(100, 80, 500, 300)
end.

Согласитесь, проще выглядит?

А теперь покажем, что эллипс созданный с помощью DrawEllipse действительно незалит. Для этого нарисуем что-нибуть, например, залитый круг процедурой FillCircle(x,y,r), а сверху незалитый эллипс, который появится через 2 секунды. Смотрим, что у нас получислось:

Код PascalABC.Net

uses
  GraphABC;

begin
  SetBrushColor(clBlue); //цвет круга
  FillCircle(200, 150, 100); //заливаем окружность
  sleep(2000); //пауза на 2 секунды
  SetPenWidth(5); //толщина границы эллипса
  SetPenColor(ClRed); //цвет границы эллипса
  DrawEllipse(20, 90, 380, 210) //рисуем границу эллипса
end.

Если известна большая ось

Если известен размер большой оси овала, то само построение в разы упрощается.

Заданную ось нужно поделить на три равные части, как на фото:

Измерить расстояние О1 и О2 – это радиус. Из этих точек провести окружности радиусом О1О2, как на фото:

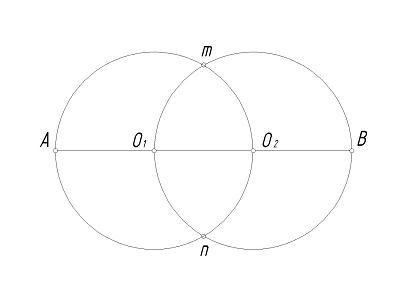
Пересечение окружностей назовем m и n.

Точки m и n с O1 и O2 соединяем, получая в итоге прямые, которые необходимо продлить до пересечения с окружностями. Точки 1, 2, 3, 4 в этом случае – точки сопряжения дуг.

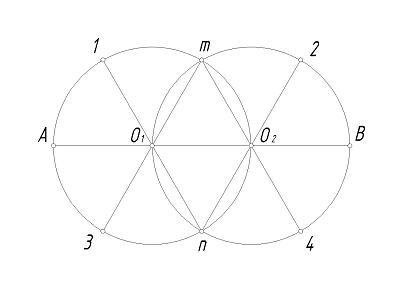
Точки m, n считаем центрами и проводим из каждой радиус максимальный, который равен n2 и m3. Получаются дуги 12 и 34. Овал нарисован, полученный результат можно сравнить с этим изображением:

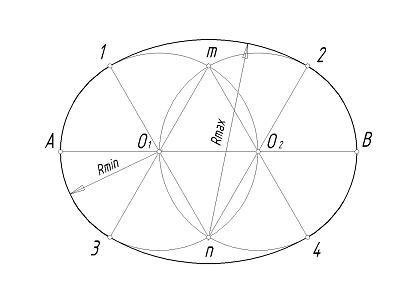
Элементы черчения для начинающих — построение эллипса техническими способами.

Первый способ начертить эллипс.

Давайте начертим эллипс, вписанный в прямоугольник А.

Сначала при помощи циркуля найдите, где круг (показанный на рисунке А)
пересекает длинную среднюю линию. Эти пересечения обозначены точками (1) и (2).

Рис. 13.5.

Воткните в эти точки булавки, а третью булавку (3) — в конце средней линии.

Крепко обвяжите эти булавки прочной льняной ниткой, как показано на рисунке
В.

Удалите булавку (3) и очертите карандашом эллипс, как показано на рисунке С. Нитка должна быть постоянно равномерно
натянута.

Второй способ построения.

Вот еще один способ как начертить эллипс, вписанный в прямоугольник А.

Рис. 13.6.

Начертите два круга с центром в точке О. Диаметр одного круга должен быть
равен ширине прямоугольника, а диаметр другого — длине прямоугольника, как
показано на рисунке D.

Теперь проведите линии наподобие спиц колеса, как показано на рисунке Е.

Через точки пересечения спиц с малым кругом проведите линии, параллельные
длинным сторонам. Через точки пересечения спиц с большим кругом проведите
линии, параллельные коротким сторонам.

Рис. 13.7.

Эллипс проходит через точки пересечения линий, параллельных коротким
сторонам и параллельных длинным сторонам, как показано на рисунке F.

Третий способ построения эллипса.

Приводим еще один способ начертить эллипс определенной величины.

Возьмите полоску бумаги и отметьте на ней половину длины данного в качестве
основы прямоугольника. Обозначьте точку буквой L, как показано на рисунке G.

Рис. 13.8.

Далее положите полоску вдоль линии ширины и буквой W обозначьте точку,
отмечающую половину этой ширины, как показано на рисунке Н.

Теперь поместите бумажную полоску так, чтобы точка L касалась линии ширины,
а точка W касалась линии длины, как показано на рисунке I.

Кончик полоски (обозначенный буквой Е) показывает, где проходит контур
эллипса.

Продолжайте двигать полоску по кругу, пока не отметите столько точек,
сколько вам нужно.

Этот метод подходит для вычерчивания эллипсов любой величины. При черчении
после обозначения точек можно вычертить контур эллипса по лекалу.

Другие свойства

Оптические
- Свет от источника, находящегося в одном из фокусов, отражается эллипсом так, что отраженные лучи пересекутся во втором фокусе.
- Свет от источника, находящегося вне любого из фокусов, отражается эллипсом так, что отраженные лучи ни в каком фокусе не пересекутся.
Если F1{\displaystyle F_{1}} и F2{\displaystyle F_{2}} — фокусы эллипса, то для любой точки X, принадлежащей эллипсу, угол между касательной в этой точке и прямой (F1X){\displaystyle (F_{1}X)} равен углу между этой касательной и прямой (F2X){\displaystyle (F_{2}X)}.
Прямая, проведённая через середины отрезков, отсечённых двумя параллельными прямыми, пересекающими эллипс, всегда будет проходить через центр эллипса. Это позволяет построением с помощью циркуля и линейки
Эквивалентная формулировка: через середины двух любых параллельных хорд эллипса проходит какой-либо диаметр эллипса. В свою очередь, любой диаметр эллипса всегда проходит через центр эллипса.

легко получить центр эллипса, а в дальнейшем оси, вершины и фокусы.
Эволютой эллипса является астроида, вытянутая вдоль вертикальной оси.
Точки пересечения эллипса с осями являются его вершинами.
Эксцентриситет эллипса, то есть отношение e=ca=1−b2a2(⩽e<1),{\displaystyle e={\frac {c}{a}}={\sqrt {1-{\frac {b^{2}}{a^{2}}}}}\;\;\;(0\leqslant e<1),}

Если эксцентриситет эллипса равен нулю (что то же самое, что фокальное расстояние равно нулю: F1F2=0{\displaystyle F_{1}F_{2}=0}), то эллипс вырождается в окружность.

характеризует вытянутость эллипса. Чем эксцентриситет ближе к нулю, тем эллипс больше напоминает окружность и наоборот, чем эксцентриситет ближе к единице, тем он более вытянут.
Экстремальные свойства
Если F{\displaystyle F} — выпуклая фигура и Tn{\displaystyle T_{n}} — вписанный в F{\displaystyle F} n{\displaystyle n}-угольник максимальной площади, то
S(Tn)≥S(F)⋅nsin⁡(2⋅π/n)2⋅π,{\displaystyle S(T_{n})\geq S(F)\cdot {\frac {n}{\sin(2\cdot \pi /n)}}{2\cdot \pi },}

где S(F){\displaystyle S(F)} обозначает площадь фигуры F{\displaystyle F}

Более того: равенство достигается в том и только в том случае, если F{\displaystyle F} ограничено эллипсом.

Среди всех выпуклых замкнутых кривых, ограничивающих данную площадь, эллипсы и только они имеет максимальную аффинную длину.

Если произвольный эллипс вписан в треугольник ABC и имеет фокусы P и Q, тогда для него справедливо соотношение

PA¯⋅QA¯CA¯⋅AB¯+PB¯⋅QB¯AB¯⋅BC¯+PC¯⋅QC¯BC¯⋅CA¯=1.{\displaystyle {\frac {{\overline {PA}}\cdot {\overline {QA}}}{{\overline {CA}}\cdot {\overline {AB}}}}+{\frac {{\overline {PB}}\cdot {\overline {QB}}}{{\overline {AB}}\cdot {\overline {BC}}}}+{\frac {{\overline {PC}}\cdot {\overline {QC}}}{{\overline {BC}}\cdot {\overline {CA}}}}=1.}

Если лестницу (бесконечно тонкий отрезок прямой) прислонить к вертикальной стенке с горизонтальным полом, и один конец лестницы будет скользить по стенке (всё время касаясь её) а второй конец лестницы будет скользить по полу (всё время касаясь его), тогда любая фиксированная точка лестницы (не на её концах), будет двигаться по дуге некоторого эллипса. Это свойство остаётся верным, если мы возьмём точку не внутри лестницы-отрезка, а на её мыслимом продолжении. Последнее свойство используется в описанном выше.mw-parser-output .ts-Переход img{margin-left:.285714em} эллипсографе.

Касательная, проходящая через точку (x0,y0){\displaystyle (x_{0},y_{0})}, принадлежащую эллипсу, имеет следующее уравнение:

xxa2+yyb2=1.{\displaystyle {\frac {xx_{0}}{a^{2}}}+{\frac {yy_{0}}{b^{2}}}=1.}

Как рисовать правильные овалы

«Ни каких рыбок и сосисок! Надо рисовать правильные овалы! »

Именно так говорил мой преподаватель — Сергей Иванович Полуйчик, когда смотрел наши первые натюрморты. Благодаря этой фразе, я сразу запомнила, как должны выглядеть правильные овалы при построении цилиндрических форм.

Итак, знакомимся с рыбками, сосисками, и правильными овалами.

РЫБКА
— неправильный овал с острыми углами.

Овал — это круг, который лежит на плоскости, поэтому с какой бы стороны мы не смотрели, у него не может быть острых углов.

СОСИСКА
— неправильно нарисованный овал с параллельными сторонами.

Еще раз чтобы запомнилось: овал — это круг на плоскости, у круга нет параллельных сторон.

ПРАВИЛЬНЫЙ ОВАЛ
, без острых углов и параллельных сторон.

Соблюдая правила перспективы, дальняя часть овала рисуется меньше (красная линия), ближняя к зрителю — больше (синяя линия на рисунке).

Практически все цилиндрические и конусовидные формы (кувшины, крынки, вазы, бутыли, кружки и т.д.) рисуются по одинаковой схеме. Вот, на примере этого кувшинчика и разберем пошагово эту схему рисования цилиндрических тел.

Всё построение делается легкими, еле заметными линиями, чтобы не пришлось стирать резинкой, так как при стирании портится верхний слой бумаги. И краска в живописи, и штрихи в рисунке ложатся на бумагу после стирания неровно.

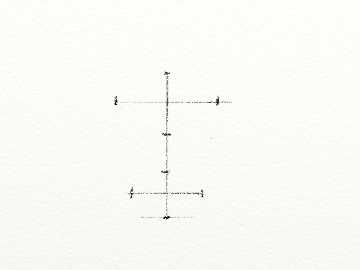
Определяем место предмета на листе. Проводим центральную осевую линию для построения кувшина.

Определяем место осевых линий для построения овалов. То есть — с помощью метода визирования, уточняем пропорции и размеры между центрами овалов у кувшина. Проводим эти линии.

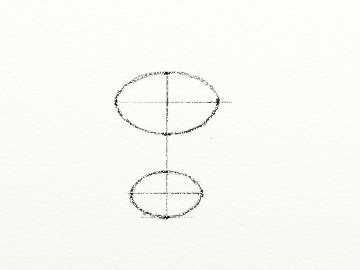
С помощью визирования определяем размер овалов. Откладываем этот размер с помощью карандаша, отмечаем одинаковые отрезки от точки пересечения центровых линий.

Откладываем точки ширины овалов.

Отмечая эти размеры не забываем о правилах перспективы: та сторона овала, что дальше от нас — будет чуточку меньше, значит та, что ближе к нам — больше.

Точно также помним, чем ниже уровня глаз находится овал, тем сильнее ему хочется стать кругом.

Наконец-то прорисовываем овалы нашего цилиндрического предмета.

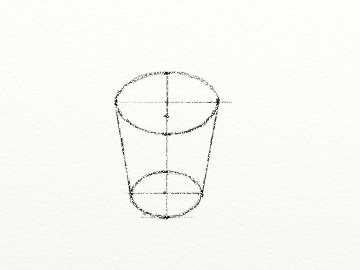
Соединяем крайние точки овалов и наш кувшин практически готов.

Осталось дорисовать ручку и носик. При рисовании ручки и носика, стараемся помнить, что обычно они находятся напротив друг друга, то есть на одной линии.

КАК РИСОВАТЬ ОВАЛЫ В ЗАВИСИМОСТИ ОТ УРОВНЯ ГЛАЗ ХУДОЖНИКА

Так будет выглядеть построение кувшина, если мы поставим его повыше, чем тот, построение которого мы разбирали.

Так будет выглядеть построение кувшина, если верхняя кромка кувшина будет находиться на уровне глаз, поэтому изображаем в виде линии. Но дно-то кувшина, ниже уровня глаз, поэтому, чтобы увидеть линию дна — строим для дна овал. рисуем кувшин выше уровня глаз

Так будет выглядеть построение кувшина, если его середина будет совпадать с линией глаз. Верхняя часть кувшина будет выше линии глаз — рисуем овал, у которого ближе к нам будет верхняя линия. Дно кувшина получается немного ниже уровня глаз, потому строим обычный овал. Но! Если кувшин (ваза) стоит далеко от зрителя (художника), то и верхний край и линия дна будут рисоваться простой прямой линией, как будто находятся на уровне глаз. Начинающие художники очень часто допускают ошибки именно при построении овалов, от чего портится впечатление от всей картины в целом.

www.mogut-vse.ru

Площадь эллипса и его сегмента

Площадь эллипса вычисляется по формуле

S=πab.{\displaystyle S=\pi ab.}

Площадь сегмента между , выпуклой влево, и вертикальной хордой, проходящей через точки (x,y){\displaystyle \left(x,\,y\right)} и (x,−y){\displaystyle \left(x,\,-y\right):}, можно определить по формуле:

S=πab2−ba(xa2−x2+a2arcsin⁡xa).{\displaystyle S={\frac {\pi ab}{2}}-{\frac {b}{a}}\left(x\,{\sqrt {a^{2}-x^{2}}}+a^{2}\arcsin {\frac {x}{a}}\right).}

Если эллипс задан уравнением
Ax2+Bxy+Cy2=1{\displaystyle Ax^{2}+Bxy+Cy^{2}=1}, то площадь можно определить по формуле

S=2π4AC−B2.{\displaystyle S={\frac {2\pi }{\sqrt {4AC-B^{2}}}}.}

Неуловимый эллипс: рисование эллипсов в перспективе — художественный блог

Определение

Другие определения

Построение цилиндра в перспективе, вид сбоку.

Теперь попробуем рисовать цилиндр в перспективе.

Команда AutoCAD Эллипс (Ellipse)

Соотношения между элементами эллипса

Как начертить эллипсы по большой оси и углу поворота окружности

Процедура DrawEllipse

Если известна большая ось

Элементы черчения для начинающих — построение эллипса техническими способами.

Первый способ начертить эллипс.

Второй способ построения.

Третий способ построения эллипса.

Другие свойства

Как рисовать правильные овалы

Площадь эллипса и его сегмента

Теперь попробуем рисовать цилиндр в
перспективе.