Калькулятор вычисления периметра и площади геометрических фигур

Обозначения

Площадь обозначается заглавной латинской буквой S (англ. Square — квадрат). Тогда площадь квадрата со стороной a см будет вычисляться по следующему правилу

S = a2

где a — длина стороны квадрата. Вторая степень указывает на то, что происходит перемножение двух одинаковых сомножителей, а именно длины и ширины. Ранее было сказано, что у квадрата все стороны равны, а значит равны длина и ширина квадрата, выраженные через букву a.

Если задача состоит в том, чтобы определить сколько квадратов стороной 1 см содержится в исходном квадрате, то в качестве единиц измерения площади нужно указывать см2. Это обозначение заменяет словосочетание «квадратный сантиметр».

Например, вычислим площадь квадрат со стороной 2 см.

Значит, квадрат со стороной 2 см, имеет площадь, равную четырём квадратным сантиметрам:

Если задача состоит в том, чтобы определить сколько квадратов со стороной 1 м содержится в исходном квадрате, то в качестве единиц измерения нужно указывать м2. Это обозначение заменяет словосочетание «квадратный метр».

Вычислим площадь квадрата со стороной 3 метра

Значит, квадрат со стороной 3 м, имеет площадь равную девяти квадратным метрам:

Аналогичные обозначения используются при вычислении площади прямоугольника. Но длина и ширина прямоугольника могут быть разными, поэтому они обозначаются через разные буквы, например a и b. Тогда площадь прямоугольника, длиной a и шириной b вычисляется по следующему правилу:

S = a × b

Как и в случае с квадратом, единицами измерения площади прямоугольника могут быть см2, м2, км2. Эти обозначения заменяют словосочетания «квадратный сантиметр», «квадратный метр», «квадратный километр» соответственно.

Например, вычислим площадь прямоугольника, длиной 6 см и шириной 3 см

Значит, прямоугольник длиной 6 см и шириной 3 см имеет площадь, равную восемнадцати квадратным сантиметрам:

В качестве единицы измерения допускается использовать словосочетание «квадратных единиц». Например, запись S = 3 кв.ед означает, что площадь квадрата или прямоугольника равна трём квадратам, каждый из которых имеет единичную сторону (1 см, 1 м или 1 км).

Периметр круга (длина окружности)

Каждый круг имеет центр. Расстояние от центра круга до любой точки, расположенной на окружности, имеет название радиус круга. Часто ученики путают понятия «круг» и «окружность» и пытаются определить площадь окружности. Это серьезная ошибка. Следует разделить в голове понятия «круг» и «окружность». У окружности нет и не может быть площади, у нее есть только длина.

Чтобы найти периметр круга, следует вычислить длину его окружности. Существует формула для нахождения длины окружности:

L = 2πr

L= 2πd

L – длина окружности

π – это число «пи», математическая константа. Она равна отношению длины окружности к длине ее диаметра. Древнее название числа «пи» – лудольфово число. Это число иррационально, его десятичное представление после точки никогда не заканчивается.

 π = 3.141 592 653 589 793 238 462 643 383 279 502

Для удобства вычислений обычно используют значение 3.14

R – это радиус окружности

D – Диаметр окружности

Итак, чтобы определить периметр круга, надо найти произведение радиуса и 2π. Если в задаче указан диаметр, то

Например, перед нами круг с радиусом 3 см. Найдем его периметр.

L= 2*3,14*3

L=6π

L=6*3.14

L = 18.84 см

P_к= 18,84 см

Ответ: 18.84 см

Круг

Окружность — это множество точек на плоскости, которые равноудалены от центра на некоторое расстояние, называемое радиусом. Многие считают круг и окружность синонимами, однако это не так. Круг — это часть плоскости, ограниченная окружностью. Вы можете отыскать периметр и площадь круга, но у окружности найти можно только длину, так как она представляет собой кривую, не имеющую площади. Длина окружности или периметр круга находятся по простой формуле:

l = 2 pi × R,

где R – радиус фигуры.

Площадь круга рассчитывается согласно следующему выражению:

S = pi R2

Круги часто встречаются в реальной жизни. В основном это основания цилиндрических и конических деталей, а также просто круглые поверхности, например, круглые столики, диски, грампластинки или катушки. Вид окружности имеют колеса, обручи или кольца. В трехмерной реальности окружность превращается в сферу, а круг — в шар. Форму этих геометрических тел имеют многие реальные и природные объекты. Благодаря своей эффективности круг охватывает максимальную площадь при минимальном периметре. Именно поэтому форму шара имеют капли, снежные комья, метеориты или планеты.

Онлайн калькулятор

Чтобы вычислить площадь прямоугольного треугольника вам нужно знать следующие параметры (либо-либо):

• длины катетов a и b
• длину гипотенузы с и длину любого из катетов (a или b)
• длину катета (a или b) и прилежащий к нему острый угол (β или α, соответственно)
• длину катета (a или b) и противолежащий к нему острый угол (α или β, соответственно)
• длину гипотенузы с и один из острых углов (α или β)

Найти площадь прямоугольного треугольника по двум катетам

Катет a = Катет b = S =

Просто введите длины двух катетов, и получите ответ.

Чему равна площадь (S) прямоугольного треугольника если известны оба катета (a и b)?

S = ½ ⋅ a ⋅ b

Пример

К примеру найдём площадь прямоугольного треугольника у которого сторона a = 2 см, а сторона b = 4 см:

S = 2 ⋅ 4 / 2 = 8 / 2 = 4 см²

Найти площадь прямоугольного треугольника по катету и гипотенузе

Гипотенуза c = Катет (a или b) = S =

Введите длины гипотенузы и одного из катетов, и получите ответ.

Чему равна площадь (S) прямоугольного треугольника если известны его гипотенуза (c) и один из катетов (a или b)?

S = ½ ⋅ a ⋅ √c² — a² = ½ ⋅ b ⋅ √c² — b²

Пример

К примеру посчитаем чему равна площадь прямоугольного треугольника у которого катет a = 2 см, а гипотенуза c = 5 см:

S = 2 ⋅ √5² — 2² / 2 = √25 — 4 ≈ 4.58 см²

Найти площадь прямоугольного треугольника по катету и прилежащему к нему острому углу

Катет (a или b) = Прилежащий угол (β или α) = ° S =

Введите длину одного из катетов и прилежащий к нему острый угол в градусах.

То есть к катету a прилежащий ∠β, а к катету b — ∠α

Чему равна площадь (S) прямоугольного треугольника если известны один из катетов (a или b) и прилежащий к нему угол?

S = ½ ⋅ a² ⋅ tg(β) = ½ ⋅ b² ⋅ tg(α)

Пример

К примеру посчитаем чему равна площадь прямоугольного треугольника у которого катет a = 4 см, а прилежащий к нему ∠β = 45°:

S = ½ ⋅ 4² ⋅ tg(45) = ½ ⋅ 16 ⋅ 1 = 16 / 2 = 8 см²

Найти площадь прямоугольного треугольника по катету и противолежащему к нему острому углу

Катет (a или b) = Противолежащий угол (α или β) = ° S =

Введите длину одного из катетов и противолежащий к нему острый угол в градусах.

То есть к катету a противолежащий ∠α, а к катету b — ∠β

Чему равна площадь (S) прямоугольного треугольника если известны один из катетов (a или b) и противолежащий к нему угол?

S = ½ ⋅ a² ⋅ tg(90 — α) = ½ ⋅ b² ⋅ tg(90 — β)

Пример

К примеру посчитаем чему равна площадь прямоугольного треугольника у которого катет a = 4 см, а противолежащий к нему ∠α = 45°:

S = 4² / 2⋅ tg(45) = 16 / 2 ⋅ 1 = 8 см²

Пример

К примеру посчитаем чему равна площадь прямоугольного треугольника у которого гипотенуза c = 8 см, а ∠α = 45°:

S = ½ ⋅ 8² ⋅ sin(45) ⋅ cos(45) ≈ ½ ⋅ 64 ⋅ 0.7071067812 ⋅ 0.7071067812 ≈ 16 см²

Решение задач

Площадь прямоугольника равна 80 см2, длина составляет 10 см. Чему равен периметр фигуры?

Как решаем:

• Для использования формулы P = 2 * (a + b), нам нужно найти ширину;
• Так как S = a * b, для поиска одной стороны необходимо разделить площадь на известную сторону: 80 : 10 = 8;
• Далее подставляем известные переменные в формулу: (10 + 8) * 2 = 36;

Ответ: 36 см.

Равнобедренный треугольник имеет периметр 40 см, длина его основания составляет 6 см. Какую длину будут иметь две другие стороны? 

Как решаем:

• Используя формулу P = a + b + c вычислим сумму двух неизвестных сторон: 40 — 6 = 34;
• Известно, что равнобедренный треугольник имеет две равные стороны;
• Далее делим получившуюся сумму на два: 34 : 2 = 17 см;

Ответ: две другие стороны равны 17см.

Круг вписан в квадрат, его сторона равна 20 см. Найти периметр круга.

Как решаем:

• Периметр круга равен длине ограничивающей его окружности. Значит P = L = d * π;
• Сторона квадрата для круга является диаметром, поэтому P = 20 * 3,14;

Ответ: 62,8 см.

Чтобы ребенок еще лучше учился в школе, запишите его на уроки математики. Лето — прекрасное время, чтобы заниматься ей с удовольствием, в комфортном темпе, без контрольных и оценок за четверть, валяясь дома на полу или за городом на травке.

Вместо скучных параграфов ребенка ждут интерактивные упражнения с мгновенной автоматической проверкой. Наши преподаватели понятно объяснят что угодно — от дробей до синусов — и ответят на вопросы, которые бывает неловко задать перед всем классом.

ремонт квартир и домов

Онлайн-калькулятор площади стен и полов

Онлайн-калькулятор считает периметр, площадь пола и стен в комнатах прямоугольной формы. Нужно ввести длину, ширину и высоту помещения. Добавить размеры окон и дверей. Окна и двери можно добавлять и удалять.

Размеры вводим в метрах, можно использовать дробные значения. Результаты получаем в погонных и квадратных метрах.

Для чего нужно высчитывать площадь стен и полов?

Площади стен и полов нужны для расчета материалов и общей стоимости работ отделочников. Цена за укладку плитки, штукатурку, стяжки, поклейку обоев и покраску выставляем в гривнях за один квадратный метр. Расход материалов считаем, умножая площадь покрытия на толщину слоя. Калькуляторы расхода материалов.

Периметр — общую длину стен комнаты — используем, чтобы узнать, во сколько обойдется монтаж и отделка багетов и плинтусов.

Какие размеры нужны для расчетов?

Для расчетов замеряем с рулеткой или лазерным дальномером:

• длину комнаты
• ширину комнаты
• высоту стен
• высоту и ширину дверных и оконных проемов

Какие инструменты применяют для расчета площадей?

Используем программу — 3D редактор

Устанавливаем на компьютер программу-редактор, например, ArchiCAD, AutoCAD, SketchUp. Рисуем комнату по размерам, получаем данные, выделяя нужные фрагменты.

Преимущество: не надо считать вручную. Удобно использовать для определения площадей в комнатах с неправильной и сложной геометрией.

Недостаток: нужно потратить время на изучение программ. И без компьютера или планшета не обойтись.

Считаем вручную

Размеры записываем на листике, смартфоне, куске гипсокартона или стене. Для расчетов используем калькулятор, табличный редактор (Exel), или считаем в столбик.

Преимущество: можно посчитать прямо на объекте, при необходимости — уточнить размеры. Достаточно иметь карандаш и умную голову.

Недостаток: легко ошибиться, пропустить размер, посчитать что-либо два раза.

Как вычислить площадь стен и полов в комнате прямоугольной формы?

В качестве примера рассмотрим комнату на рисунке ниже.

Размеры снимаем в метрах. Потом при умножении получаем метры квадратные или погонные.

Для расчета стоимости работ достаточно точности до 1 см (два знака после запятой). Например: длина комнаты 5,62 м.

Полученные данные записываем в удобной для нас форме. Кому сподручнее листок бумаги, кому — компьютер.

Имея на руках данные о размерах, приступаем к расчетам с помощью пальцев, бумажки или программы Microsoft Excel.

Как рассчитать площадь пола и потолка

Чтобы узнать площадь пола или потолка, умножаем длину комнаты на ее ширину, и получаем результат в м 2 (квадратных метрах).

S_пола = Длина × Ширина

Как рассчитать периметр — общую длину стен

Чтобы высчитать периметр комнаты (общую длину стен), к длине комнаты прибавляем ее ширину и полученный результат умножаем на два. Результат вычислений дает нам длину стен в м. п. (метрах погонных). Периметр — это длина багетов в комнате.

P = (Длина + Ширина)×2

Как рассчитать площадь стен

Немножко сложнее рассчитать площадь стен комнаты. Для этого периметр комнаты умножаем на ее высоту и из полученного результата вычитаем площадь оконных и дверных проемов.

• P — периметр стен помещения
• H — высота стен помещения
• S_д — площадь всех дверей помещения
• S_о — площадь всех окон помещения

Полученные данные можем использовать в смете ремонта квартиры в Киеве онлайн.

Если считать в столбик — это скучно и долго, вводим данные в Онлайн-калькулятор площади стен и полов, нажимаем «Enter» и сразу получаем результат.

Когда комната имеет неправильную форму, делим её на множество прямоугольников, находим площадь каждого из них, а затем суммируем.

Как посчитать периметр комнаты для покупки отделочных материалов

При ремонте в квартире или доме возникает момент, когда нужно знать, какое количество материала требуется закупить

Чтобы не ошибиться с объемом, важно знать, как посчитать периметр комнаты, ее стен, пола и других поверхностей

Расчет количества обоев

Этот вопрос возникает практически в самом начале ремонта, ведь хочется купить правильное количество рулонов, чтобы не испытывать нехватку, но и не переплачивать за лишнее. А значит, нужно знать, как посчитать периметр комнаты.

Что вообще такое периметр, все помнят из школьного курса – это сумма длин всех сторон. Если мы говорим о комнате, то – стен. Итак, для расчета периметра требуется выяснить длину всех стен. Сделать это очень легко: необходимо измерить две смежные и результат увеличить вдвое. К примеру, если одна стена имеет длину 4 метра, другая 6, то ее периметр равняется 20 м: 2х(4+6)=20.

Теперь требуется вычислить, сколько рулонов нужно закупить на такую комнату

В этой ситуации важно не только знать, как посчитать периметр комнаты, но и понимать, что необходимо еще и знание высоты потолка. Предположим, что в данном случае комната имеет стандартную высоту – 2.5 метра

Далее вычисляют количество обоев, которые требуется приобрести. Сегодня все большей популярностью пользуются обои, ширина которых составляет 1 метр. Возьмем для примера именно такой вариант. Длина рулона остается стандартной – 10 метров.

Теперь, имея всю необходимую информацию, высчитать нужное количество обоев совсем не сложно.

Лучше всего показать на образце, как посчитать периметр комнаты. Примеры – оптимальный вариант для большинства покупателей. Итак, при наших размерах, из одного рулона обоев получится четыре полосы материала (10:2.5). Эти четыре полосы займут четыре метра из нашего периметра, поскольку ширина их – 1 м. Значит, чтобы высчитать количество рулонов, нужно периметр разделить на количество метров, которые покрывает один рулон обоев: 20/4=5. Выходит, нам требуется пять рулонов обоев.

Важно знать: если в результате последнего действия получилось не целое число, округлять его необходимо в большую сторону, даже если десятых долей мало. То есть, если выходит, что приобретать нужно 5.15 рулонов, требуется купить 6

Иначе эти 15 сантиметров просто нечем будет заклеить.

Погрешности

При нашем расчете мы воспользовались знанием о том, как посчитать периметр комнаты, однако не учли другие факты – наличие двери и окна. Поэтому, рассчитывая, сколько обоев нужно купить, не забывайте убавлять их на необходимое количество полос.

Покрытие пола

Для покупки половых покрытий тоже важно знать, как посчитать периметр комнаты. Формула все та же: сумма длин всех сторон

При этом нет необходимости обращать внимание на двери и окна. Достаточно либо измерить две смежные стороны и умножить на два, либо измерить каждую сторону комнаты и сложить эти цифры

Рассчитать покрытие для пола, зная периметр и длины, будет совсем не сложно. Зачастую на сайтах, продающих эти самые покрытия, имеются специальные калькуляторы. В них необходимо ввести длину и ширину комнаты, желаемое покрытие. После этого появится информация о том, сколько материала необходимо приобретать. Если речь идет о линолеуме, то варианты его ширин соответствуют стандартным торцевым сторонам комнаты. Поэтому покупают его, исходя из длины комнаты.

Если покупать кафель, паркет или ламинат, необходимы более сложные расчеты. Вероятно, для этого лучше воспользоваться помощью менеджеров, работающих в строительном магазине или торговой точке, где вы будете покупать покрытие.

Потолочное покрытие

Этот материал рассчитываю аналогично предыдущему способу. Если речь идет о натяжных или подвесных потолках, тут еще проще – все сделают специально обученные люди, которые совершенно бесплатно приезжают на замеры перед заключением договора с компанией.

Как видите, у вас не должно возникнуть особых проблем с расчетами. Удачи!

Задания для самостоятельного решения

Задача 1. Длина прямоугольника составляет 6 см, а ширина 2 см. Найдите периметр.

Решение

P = 2(a + b)

a = 6, b = 2P = 2(6 + 2) = 12 + 4 = 16 см

Ответ: периметр прямоугольника равен 16 см.

Задача 2. Длина прямоугольника составляет 6 см, а ширина 2 см. Найдите площадь.

Решение

S = aba = 6, b = 2S = 6 × 2 = 12 см2

Ответ: площадь равна 12 см2.

Задача 3. Площадь прямоугольника составляет 12 см2. Длина составляет 6 см. Найдите ширину прямоугольника.

Решение

S = abS = 12, a = 6, b = x12 = 6 × xx = 2

Ответ: ширина прямоугольника составляет 2 см.

Задача 4. Вычислите площадь квадрата со стороной 8 см

Решение

S = a2a = 8S = 82 = 64 см2Ответ: площадь квадрата со стороной 8 см равна 64 см2

Задача 5. Вычислите объем прямоугольного параллелепипеда, длина которого 6 см, ширина 4 см, высота 3 см.

Решение

V = abca = 6, b = 4, c = 3V = 6 × 4 × 3 = 72 см3.

Ответ: объем прямоугольного параллелепипеда, длина которого 6 см, ширина 4 см, высота 3 см равен 72 см3

Задача 6. Объем прямоугольного параллелепипеда составляет 200 см3. Найдите высоту параллелепипеда, если его длина равна 10 см, а ширина 5 см

Решение

V = abcV = 200, a = 10, b = 5, c = x200 = 10 × 5 × x200 = 50xx = 4

Ответ: высота прямоугольного параллелепипеда равна 4 см.

Задача 7. Площади земельного участка, засеянные пшеницей и льном, пропорциональны числам 4 и 5. На какой площади засеяна пшеница, если под льном засеяно 15 га

Решение

Число 4 отражает площадь, засеянную пшеницей. А число 5 отражает площадь, засеянную льном.
Сказано что площади, засеянные пшеницей и льном пропорциональны этим числам.

Проще говоря, во сколько раз изменяются числа 4 или 5, во сколько же раз изменится и площадь, которая засеяна пшеницей или льном. Льном засеяно 15 га. То есть число 5, которое отражает площадь, засеянную льном, изменилось в 3 раза.

Тогда число 4, которое отражает площадь засеянную пшеницей, нужно увеличить в три раза

4 × 3 = 12 га

Ответ: пшеницей засеяно 12 га.

Задача 8. Длина зернохранилища 42 м, ширина составляет длины, а высота – 0,1 длины. Определите сколько тонн зерна вмещает зернохранилище, если 1 м3 его весит 740 кг.

Решение

a — длинаb — ширинаc — высота

a = 42 мb = мc = 42 × 0,1 = 4,2 м

Определим объем зернохранилища:

V = abc = 42 × 30 × 4,2 = 5292 м3

Определите сколько тонн зерна вмещает зернохранилище:

5292 × 740 = 3916080 кг

Переведём килограммы в тонны:

Ответ: зернохранилище вмещает 3916,08 тонн зерна.

Задача 9. 12. Бассейн имеет форму прямоугольного параллелепипеда, длина которого равна 5,8 м, а ширина – 3,5 м. Две трубы наполняют его водой в течение 13 ч 32 мин., причём через одну из них вливается 25 л/мин, а через вторую – 0,75 этого количества. Определите высоту (глубину) бассейна.

Решение

Определим сколько литров в минуту вливается через вторую трубу:

25 л/мин × 0,75 = 18,75 л/мин

Определим сколько литров в минуту вливается в бассейн через обе трубы:

25 л/мин + 18,75 л/мин = 43,75 л/мин

Определим сколько литров воды будет залито в бассейн за 13 ч 32 мин

43,75 × 13 ч 32 мин = 43,75 × 812 мин = 35 525 л

1 л = 1 дм3

35 525 л = 35 525 дм3

Переведём кубические дециметры в кубические метры. Это позволит вычислит объем бассейна:

35 525 дм3 : 1000 дм3 = 35,525 м3

Зная объём бассейна можно вычислить высоту бассейна. Подставим в буквенное уравнение V=abc имеющиеся у нас значения. Тогда получим:

V = 35,525a = 5.8b = 3.5c = x

35,525 = 5,8 × 3,5 × x35,525 = 20,3 × xx = 1,75 м

с = 1,75

Ответ: высота (глубина) бассейна составляет 1,75 м.

Понравился урок? Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках

Как найти периметр прямоугольника, зная его площадь?

Как найти периметр прямоугольника, зная его площадь?

1. периметер p=2*a+(2*s)/a, где а от 0 до s
2. Чтобы найти периметр прямоугольника надо сложить все его стороны.
3. Периметр может быть от 4*корень (S) до бесконечности.
4. Встречный вопрос — в доме 40 квартир — сколько это этажей? — емкость в 1 литр — какой диаметр емкости?

   Продолжить?…

5. плюс минус при подборе вручную по формуле будет иногда разницы втрое
6. решить систему уравненийодно из которых — формула площади второе формула периметра
7. S=a*b=к примеру 45см ^2

   разложим на простые множители 45

   45/3=1515/3=5

   5/5=1

   НОД=1

   Р=2(3^2+5^1)=2(9+5)=28

   P.S. Как разложить число на простые множители см.

8. Ни по какой. Вариантов будет бесконечное множество
9. Прямоугольник это четырхугольник, у которого четыре прямых угла. Размеры прямоугольника задаются длиной его сторон, обозначаемых обычно a и b. Прямоугольник, все стороны которого равны (a=b) называется квадратом. Свойства прямоугольника противолежащие стороны равны и параллельны друг другу; диагонали равны и в точке пересечения делятся пополам; сумма квадратов диагоналей равна сумме квадратов всех (четырех) сторон. Периметр P прямоугольника равен удвоенной сумме сторон, прилежащих к одному углу P = 2(a + b). Длина диагонали d прямоугольника вычисляется по теореме Пифагора: d = #8730;(a2 + b2). Углы между диагоналями прямоугльника определяются соотношением сторон: #945; = 2arctg(a/b), #946; = 2arctg(b/a), #945; + #946; = 180. Площадь S прямоугольника равна произведению сторон, прилежащих к одному углу: S = ab. Также можно выразить площадь прямоугольника через длину диагоналей и угол между ними: S = d2sin(#945;/2)cos(#945;/2). Радиус описанной вокруг прямоугольника окружности равен половине длины диагонали: R = #8730;(a2 + b2)/2.

   В прямоугольник (если он не квадрат) нельзя вписать окружность так, чтобы она касалась всех его сторон. Максимальный радиус окружности, которая может поместиться внутри прямоугольника, равен половине его меньшей стороны.

10. этого не достаточно. Надо еще знать одну из сторон
11. надо решить систему уравнений например если пл-дь равна 16, то ситема примет вид. при учете что х это периметр, а и в стороны прямоугольника, то а*в=16 2а+2в=х отсюда верхнее уравнее системы можно выразить одну сторну через другую и подставить в нижнее уравнение, например: а=16/в то 2(16/в) +2в=х

    вот только надо знать сторону хоть одну чтобы определить вторую, а строна в как как писал выше Aqni имеет значения почти от нуля и почти до S внашем почти до 16….пиши мне на мыло если не понятно до сих пор )

Инструменты для определения квадратных метров

Для расчета площади стен потребуются:

• Строительный уровень, помогает удостовериться в ровном расположении меток, линий.
• Чтобы правильно вычислить площадь, потребуется рулетка.
• Используя угольник, можно удостовериться в правильности углов.

Проверка угла

• На бумаге карандашом чертят чертеж.
• Для точности подсчета, лучше пользоваться калькулятором.

Рисуем схематическое изображение перегородок в комнатах, наносим на чертеж размеры, измеренные рулеткой. Не забудьте обозначить проемы окон, дверей на внешних стенах.

Недостаток расчетов вручную стен в ванной – легко допустить ошибку, пропустив замер одной из сторон. Либо наоборот, посчитать одну сторону два раза.

Вариант расчета – программа 3Д Редактор. Нужно загрузить из интернета на компьютер. Достаточно вбить в поиск 3Д редактор, система предложит варианты.

В программе необходимо нарисовать схематический рисунок комнаты в квартире, указать размеры стен, выемок, выпуклостей. Выделив необходимые участки, получаем точные расчеты размеров.

Схематическое изображение на 3Д редакторе

Как найти периметр и площадь?

Интересно, что много лет назад такой раздел математики, как «геометрия» называли «землемерием». И о том, как найти периметр и площадь, известно уже давно. К примеру, говорят, что самыми первыми вычислителями этих двух величин являются жители Египта. Благодаря таким знаниям они могли строить известные сегодня сооружения.

Умение находить площадь и периметр может пригодиться в повседневной жизни. В быту данные величины используются, когда необходимо что-либо покрасить, засадить или обработать сад, поклеить в комнате обои и т. п.

Периметр

Чаще всего необходимо узнать периметр многоугольников или треугольников. Чтобы определить эту величину, достаточно лишь знать длины всех сторон, а периметр составляет их сумму. Найти периметр, если известна площадь, также возможно.

Треугольник

Если необходимо знать периметр треугольника, для его вычисления стоит применить такую формулу P = а + b + с, где а, b, с — стороны треугольника. В этом случае все стороны обычного треугольника на плоскости суммируются.

Периметр круга обычно принято называть длиной окружности. Чтобы узнать данную величину, необходимо использовать формулу: L = π*D = 2*π*r, где L- длина окружности, r — радиус, D — диаметр, а число π, как известно, примерно равно 3,14.

Формулы для периметров квадрата и ромба одинаковы, потому что и у одной фигуры, и у другой все стороны равны. Поскольку квадрат и ромб имеют равные стороны, то их (стороны) можно обозначить одной буквой «а». Получается, периметр квадрата и ромба равен:

Р = а + а + а + а или Р = 4а

Прямоугольник, параллелограмм

У прямоугольника и параллелограмма противолежащие стороны одинаковы, поэтому их можно обозначить двумя разными буквами «а» и «b». Формула выглядит так:

Р = а + b + а + b = 2а + 2b. Двойку можно вывести за скобки, и получится такая формула: Р = 2 (а+b)

Трапеция

У трапеции все стороны разные, поэтому их обозначают разными буквами латинского алфавита. В связи с этим формула для периметра трапеции выглядит так:

Р = а + b + с + d Здесь все стороны суммируются вместе.

Дополнительно о вычислении периметра можно узнать из статьи Как найти периметр.

Прямоугольник

Чтобы вычислить площадь прямоугольника, необходимо умножить значение одной стороны (длины) на значение другой (ширины). Если значения длины и ширины обозначаются буквами «а» и «b», то площадь вычисляется по формуле:

Ромб

Формула нахождения площади ромба имеет немного другой вид: S = a*ha, где ha – это длина высоты ромба, которая проведена к стороне.

Кроме того, площадь ромба можно узнать по формулам:

• S = a2*sin α, при этом а является стороной фигуры, а угол α — угол между сторонами;
• S = 4r2/sin α, где r — радиус вписанной в ромб окружности, а угол α — угол между сторонами.

Трапеция

Чтобы вычислить площадь трапеции, можно воспользоваться данной формулой:

S = 1/2*a*b*h, где a, b — основания трапеции, h — высота.

Треугольник

Для нахождения площади треугольника воспользуйтесь одной из нескольких формул:

• S = 1/2*a*b sin α (где а, b — стороны треугольника, а α — угол между ними);
• S = 1/2 a*h (где а — основание треугольника, h — опущенная к нему высота);
• S = abc/4R (где a, b, c — стороны треугольника, а R — радиус описанной окружности);
• S = p*r (где p — полупериметр, r — радиус вписанной окружности);
• S= √ (p*(p-a)*(p-b)*(p-c)) (где p — полупериметр, a, b, c — стороны треугольника).

Параллелограмм

Для вычисления площади данной фигуры необходимо подставить значения в одну из формул:

• S = a*b*sin α (где а, b — основания параллелограмма, α — угол между сторонами);
• S = a*ha (где a — сторона параллелограмма, ha – это высота параллелограмма, которая опущена к стороне а);
• S = 1/2 *d*D* sin α (где d и D — диагонали параллелограмма, α — угол между ними).

Как вычислить периметр прямоугольного квадратного и круглого потолка

Как правило, осуществляя ремонт, человек в основном затрачивает массу физических сил. Однако, наряду с физическим трудом, активно применяется и труд умственный.

Например, необходимо делать расчеты. Они необходимы для того, чтобы можно было рассчитать точное количество строительного материала.

Малое количество материала способствует сбою рабочего графика, ну а чрезмерно большое количество, делает ремонт достаточно затратным делом.

В расчеты входит вычисление площади и периметра (измерению подвергаются стены, потолок и пол). О том, как найти периметр, стоит поговорить подробнее.

Наиболее просто расчеты делаются в комнате имеющей форму прямоугольника или квадрата: для осуществления этой операции понадобятся примитивные школьные знания. В случае с помещениями, которые имеют форму многоугольника, трапеции и других сложных фигур, дело обстоит гораздо сложнее.

Целесообразность проведения расчетов

Наиболее часто расчеты необходимы при установке потолка из гипсокартона. Для этого нужно приобрести несколько типов материалов.

Если не делать расчеты, то возникает огромный риск сделать ошибку (ошибаются даже те, кто обладает большим опытом создания подобных конструкций).

Например, зачастую при определении периметра “на глазок”, часто не хватает материала.

Для того, чтобы узнать общую длину пристенного профиля, необходимо просуммировать все длины стен, которые образуют помещение. Часто этот потолочный профиль используют для того, чтобы создать обрешетку.

Следует закупать несколько большее материала (допустимая норма 10-15%). Если же имеется чертеж либо эскиз, то материал необходимо закупать без излишков.

Установка натяжного потолка также требует проведения расчетов. Это позволит наиболее точно учесть предстоящие расходы.

Периметр комнаты в форме прямоугольника (условно говоря, длина комнаты равняется 5 метрам, ну а ширина 2,5 метрам), рассчитывается по следующей формуле: P = 2 х 5 + 2 х 2,5 = 10 + 5 = 15.

Площадь комнаты (например, длина ее стен равняется 5 метрам), которая имеет форму квадрата, измеряется по следующей формуле:  P = 4 (число стен) х 5(длина одной стены) = 20 метров.

Периметр комнаты имеющей форму прямоугольника и форму квадрата рассчитать достаточно просто. Однако, периметр комнаты имеющую более сложную форму, найти достаточно трудно.

Как высчитать площадь комнаты, имеющей ниши и выступы

Для того, чтобы узнать площадь такого помещения, нужно замерить стены этой комнаты. Ниши и выступы разбиваются на участки, а после определяется их суммарная длина.

Как рассчитать площадь комнаты с косыми углами?

Посчитать площадь комнаты можно по такому же принципу, как в случае с нишами и выступами. Берется рулетка, и делаются измерения протяженности всех стен комнаты.

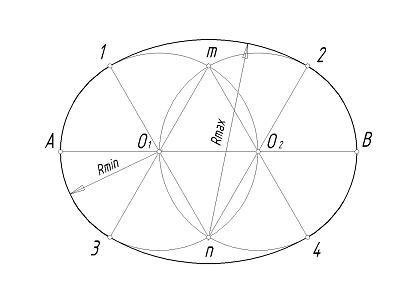
Овальная или круглая комната: как определить площадь?

Для определения периметра такой комнаты, важно вспомнить школьный курс геометрии. Формула, позволяющая узнать периметр окружности, выглядит следующим образом:. В данной формуле за P берется периметр комнаты, π-число пи, имеющее статичное значение 3,14 на а R-радиус

Радиус определяется с помощью замера диаметра площади, простирающейся двух стен, расположенных напротив друг друга

В данной формуле за P берется периметр комнаты, π-число пи, имеющее статичное значение 3,14 на а R-радиус. Радиус определяется с помощью замера диаметра площади, простирающейся двух стен, расположенных напротив друг друга.

Периметр овальной комнаты можно рассчитать воспользовавшись расчетами по эллипсу. Эта формула выглядит следующим образом:

P = π х (a + b).

В данной формуле a, b это полуоси эллипса

Говоря другими словами, для того, чтобы узнать площадь овальной комнаты, важно рассчитать самый короткий и самый длинный радиусы (они составляют расстояние от центра к краю)

Четко зная формулы, рассчитать площадь сложных фигур не является большой проблемой

Важно точно и правильно считать и уметь верно делать замеры

Вывод

Как показывает практика, узнать ответ на вопрос ” как вычислить периметр ” комнаты, имеющей форму прямоугольника или квадрата, не составляет особого труда. Помещения же, имеющие сложные формы требуют более сложных и точных расчетов.

Приходится считать не только “основные” стороны но и разного рода ниши и выемки. С комнатами, которые выполнены в форме овала или круга, считать приходится радиус и диаметр.

Для успешного расчета важно верно делать замеры и уметь правильно считать. В случае, если расчеты сделаны неверно, пригодятся 10-15 процентов заранее запасенного материала

Таблица квадратов

В жизни часто приходиться находить площади различных квадратов. Для этого каждый раз требуется возводить исходное число во вторую степень.

Квадраты первых 99 натуральных чисел уже вычислены и занесены в специальную таблицу, называемую таблицей квадратов.

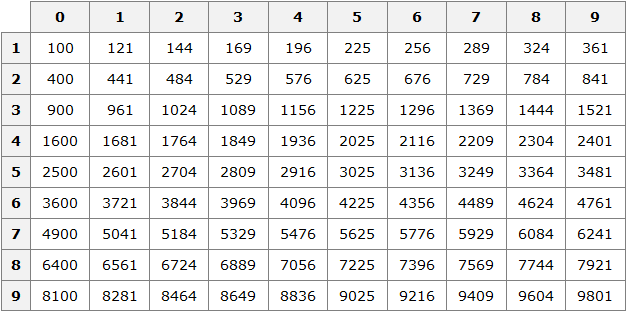
Первая строка данной таблицы (цифры от 0 до 9) это единицы исходного числа, а первый столбец (цифры от 1 до 9) это десятки исходного числа.

Например, найдём квадрат числа 24 по данной таблице. Число 24 состоит из цифр 2 и 4. Точнее, число 24 состоит из двух десятков и четырёх единиц.

Итак, выбираем цифру 2 в первом столбце таблицы (столбце десятков), а цифру 4 выбираем в первой строке (строке единиц). Затем, двигаясь вправо от цифры 2 и вниз от цифры 4, найдём точку пересечения. В результате окажемся на позиции, где располагается число 576. Значит, квадрат числа 24 есть число 576

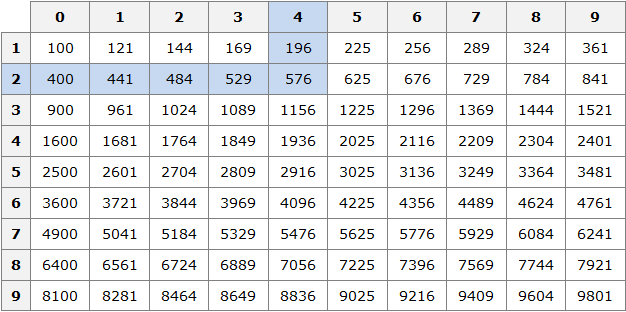
242 = 576